ナンプレ上級の行き詰まりを打破！解けない壁を超える論理テクニック

「あれ、ここから全く進まない……」 上級レベルのナンプレに挑戦していると、突然そんな理不尽な壁にぶつかることってありますよね。盤面を何度見渡しても、単純な消去法だけでは数字が埋まらない。

まさにナンプレ上級特有の行き詰まりを感じて、焦りやモヤモヤを抱えている方も多いのではないでしょうか。実は、そこから先へ進むには、これまでよりも「候補の情報を整理して可視化する視点」や、少し踏み込んだ論理テクニックが効いてきます。

この記事では、そんな「見えない壁」を突破するための具体的な考え方やコツについて解説していきます。次の一手がどうしても見つからない時に試すべき方法を知れば、難問でも糸口がつかめるようになるはずです。

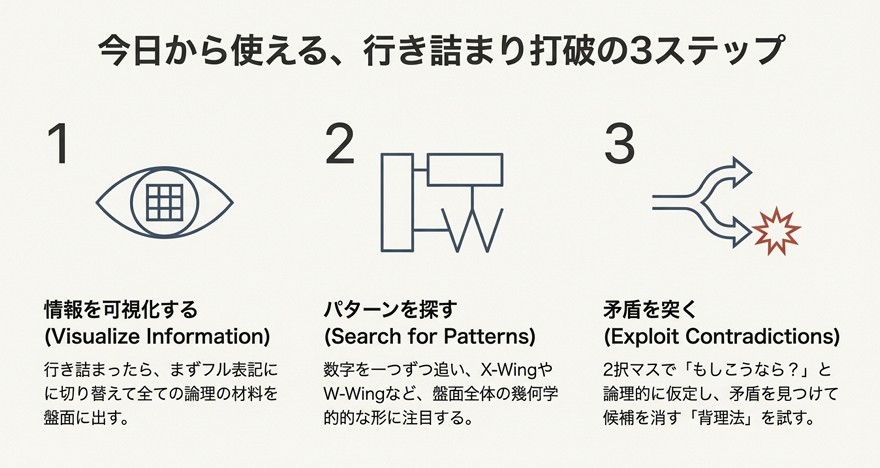
ナンプレ上級の行き詰まりを打破する基本戦略

ここでは、上級問題で手が止まってしまう根本的な理由と、それを乗り越えるための基礎的なアプローチについて解説します。ただ数字を眺めるだけでなく、情報の整理方法を見直すところから始めていきましょう。

次の一手がどうしても見つからない原因

上級問題で行き詰まる原因は、単なる注意力不足や「見落とし」だけではありません。多くの場合は、「候補の情報が不足している（または整理されていない）」ために、盤面の関係性が見えなくなることが大きいです。

単純な排除法（Scanning）の限界

中級レベルまでは、盤面を見渡して「この列で3が入るのはここだけ」「このブロックで1が入るのはここだけ」といった、いわゆる排除法（スキャン）だけで進める場面が多いですよね。これは、盤面の確定数字が直接的なヒントになりやすい構造になっているためです。

上級者が直面する「見えない数字」の壁

しかし、上級レベルになると、こうした分かりやすい確定手が表面に出にくくなります。代わりに必要になるのが、「候補同士の連鎖（チェーン）」や「配置パターン（幾何学的な形）」を読み解く力です。

これらは「もしAがここに入ればBはあそこ、するとCは……」という風に、複数手にわたる関係性を追う必要があります。これを頭の中だけで保持し続けるのは多くの人にとって負荷が大きく、途中で条件を取り違えやすくなります。つまり、適切に候補をメモして可視化しないと、論理の材料そのものが不足して「何も見えない状態（行き詰まり）」に陥りやすいんですね。

メモの使い分けとスナイダー表記の限界

皆さんは「スナイダー表記」というメモの取り方をご存知でしょうか？ 候補を書き込みすぎず、必要な情報だけを残す発想で知られている手法で、愛用している方も多いと思います。

スナイダー表記とは？

これは、3×3のブロック内で「ある数字が入る場所が2箇所に限られる場合のみ」小さくメモをする手法です。例えば、あるブロック内で「7」が入る場所が2つしかなければ、その両方に小さく「7」と書きます。

スナイダー表記のメリット

• 盤面が数字で埋め尽くされないので、視認性が高い。
• ブロック内の「2箇所に限られる候補」が見えるため、ペア系の糸口を拾いやすい。
• 必要最低限の情報で中盤までテンポよく進めやすい。

なぜ行き詰まりの原因になるのか

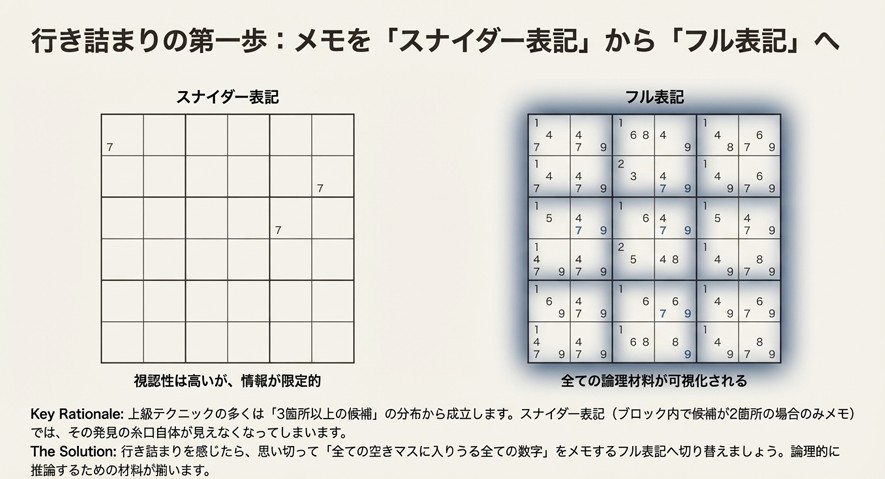
ですが、上級問題での「行き詰まり」では、このスナイダー表記が情報不足になることがあります。なぜなら、上級テクニックの多くは「3箇所以上の候補」も含めた分布から成立することが珍しくないからです。

例えば、後述するソードフィッシュは、各行（または列）に候補が2つに限定されていなくても、全体として「特定の3行の候補が3列の中に収まる」形になれば成立します。スナイダー表記にこだわりすぎると、「2択ではない候補」が盤面上に見えないため、成立しているはずのパターンが探索対象から外れてしまうことがあります。結果として、「解法があるのに見つけにくい」という状態になり、手が止まりやすくなるのです。

解決策：フル表記への移行

行き詰まりを感じたら、思い切って「全ての空きマスに入りうる全ての数字」をメモするフル表記へ切り替えましょう。盤面はごちゃごちゃしますが、論理的に推論するための材料が揃い、スナイダー表記では拾いにくかった突破口が見つけやすくなります。

井桁理論やX-Wingを発見するコツ

「ナンプレ 上級 行き詰まり」で検索すると必ず出てくるのがこのX-Wing（井桁理論）ですよね。名前は難しそうですが、理屈がわかればパズルとして楽しみながら見つけられるようになります。

X-Wingの構造とメカニズム

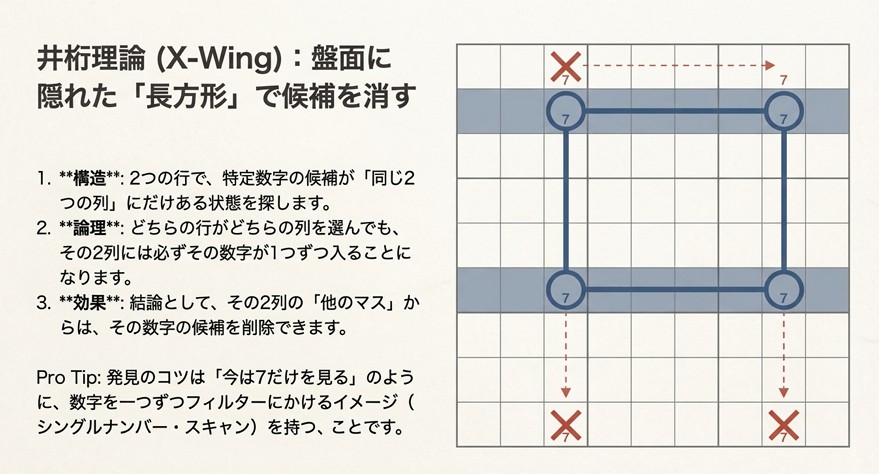
特定の数字（例えば7）に注目したとき、ある2つの行（または列）において、7が入る候補が「同じ2列（または行）」にしか存在しない状態を探します。これを線で結ぶと長方形（井桁）の形になります。

項目	詳細説明
構造	2つの行（例：行2と行5）において、数字「7」の候補が、共通する2つの列（例：列3と列8）にしか存在しない状態。
論理	行2の7は列3か列8のどちらか、行5の7も列3か列8のどちらかになります。どちらの行がどちらの列を選んでも、列3と列8には必ず7が1つずつ入ることになります。
効果	結論として、列3と列8の7は行2か行5のどちらかに必ず置かれるため、その2列の「行2と行5以外」の場所から7を削除できる。

実戦的な発見テクニック

発見のコツは、盤面全体を漫然と見るのではなく、数字を一つずつフィルターにかけるイメージ（シングルナンバー・スキャン）を持つことです。

「今は7だけを見る」と決めて、候補メモを見ながら「この行（または列）では7が入れそうなマスが2つしかない」という場所を探します。見つけたら、他の行（または列）にも「同じ列位置に7の2候補が並ぶ行（または列）はないか？」と照合していくのです。アプリであれば、該当数字をハイライトする機能を使うと見つけやすくなります。

また、テクニック名や形が頭に入りにくいときは、語呂合わせやイメージ連想で「記憶のフック」を作ると定着しやすいです（例：国際信号旗の組み合わせの覚え方（語呂合わせ・イメージ連想）のように、形と意味を結び付ける暗記法）。

浜田ロジックと呼ばれる解き方の正体

日本のナンプレ愛好家の間でよく耳にする「浜田ロジック」。一般にはW-Wingとして説明されることが多く、考え方として非常に近い（またはW-Wingの枠組みで整理できる）テクニックとして扱われます。

W-Wing（浜田ロジック）の構造

これは「離れた場所にある同じペア（例えば3と8の2択マス）」を、別の数字の「強いリンク」で繋ぐことで排除を行う手法です。日本では「ネコとネズミ排除」など、別名で語られることもあります。

W-Wingの発動条件と手順

• 条件1：盤面の離れた位置に、全く同じ候補ペア（例：どちらも[3, 8]が入るマス）が2つある。
• 条件2：その2つのマスを、ペアの片割れ（例：3）の「強いリンク（ある行・列・ブロック内で、その数字の候補が2箇所に限られる状態）」が繋いでいる。
• 結論：リンクに使われなかった方の数字（例：8）は、両方のペアマスから同時に見える位置にあるマスには入らない（候補から削除できる）。

論理としては、「もし両方のペアマスが8だと仮定すると、強いリンク側（3）の置き場がなくなって矛盾する」という背理法的な整理になります。形が見つかると候補が一気に減ることがあるので、上級の突破口として覚えておく価値が高いテクニックです。

背理法や仮定法は邪道な攻略法なのか

「どうしても解けないから、仮にここを5として進めてみよう……」 このいわゆる「仮置き」や「背理法」について、ズルをしているような罪悪感を持つ方もいるかもしれません。「論理で解いてないじゃないか」と感じてしまう気持ち、分かります。

上級者も使う「先読み（Look-ahead）」の正当性

ですが、論理的な裏付けのある仮定は、立派な戦略の一つです。特に「2択のマス」を使って、「もしAならこうなる、もしBならこうなる」と数手先まで追い、矛盾が生じるかを確認するのは、Chain（連鎖）やForcing Chainといった連鎖系の考え方にも繋がります。

数独（ナンプレ）は、ルールに従って矛盾なく埋めていく論理パズルです。

（出典：株式会社ニコリ『数独の遊び方、ルール、解き方』）

そのため、「仮定して矛盾を導く」プロセス自体は数学の証明（背理法）と同じ発想で、決して当てずっぽうではありません。ポイントは、仮定を置いたら必ず“矛盾を見つけるために”追い、矛盾が出たら候補を消す、という手順を守ることです。

当てずっぽう（Bifurcation）との違いに注意

ただし、根拠なく適当な数字を入れて「運良く解けるまで進む」やり方は、論理パズルとしての楽しみを薄めやすいです。あくまで「矛盾を導き出して候補を消す」ための手段として使うのがおすすめです。

ナンプレ上級で行き詰まりを感じた時の応用技

ここからは、さらに難易度の高い局面を打開するための、少しマニアックですが知っておくと強力な武器になるテクニックやツールを紹介します。

隠れたペアやトリプルを見落とす原因

フル表記でメモを埋め尽くした後に陥りやすいのが、情報過多で見落としが発生するパターンです。特に「隠れたペア（Hidden Pair）」は要注意です。

数字の海に溺れないために

これは、あるユニット（ブロック・行・列）の中で「数字の3と7はこの2箇所にしか入らない（ただしその2マス自体には他の候補も書かれている）」という状態です。メモ上では[1,3,5,7]と[3,5,7,9]のように他の数字も並ぶため、見た目だけだと「3と7のペア」が埋もれてしまうんですよね。

これを防ぐには、メモを書いた後に「このブロック（または行・列）の中で、この数字が入れる場所はどこ？」という逆引きの視点（各数字ごとの分布確認）で再チェックすることが大切です。「あれ、よく見たら3と7はここだけじゃん！」という発見が、ブレイクスルーに繋がります。

ソードフィッシュなど魚系テクニック

X-Wing（2行2列）を拡張した代表例が、このソードフィッシュ（Swordfish）です。こちらは「3行3列（または3列3行）」の関係になります。

3次元的な排除のロジック

3つの行（Base Set）において、特定の数字の候補が、合計として共通する3つの列（Cover Set）の中に収まっている状態を指します（各行の候補数は1〜3など、状況により異なります）。成立すれば、その「3つの列」上の、対象となる3行以外の場所から候補を削除できます。

魚系テクニックの系譜

ちなみに、さらに拡張すると「ジェリーフィッシュ（4行4列）」もあります。ただ、実戦でこれが必要になるケースは多くはなく、そこまで来ると後述するAICなどの連鎖系が先に見つかることもあります。

XYZウィングなど連鎖系解法の考え方

XY-Wing（3つのマスが連鎖する形）の発想を広げた形として知られるのがXYZ-Wingです。中心となるマス（ピボット）が3つの候補（X,Y,Z）を持っていて、周囲の2つのマスと連携して候補を絞り込みます。

論理のネットワークを構築する

このあたりの「Wing系」テクニックや、さらに高度な「AIC（Alternating Inference Chain）」といった連鎖理論を理解すると、盤面上の候補が単なる点ではなく、線で繋がったネットワークのように見えてきます。

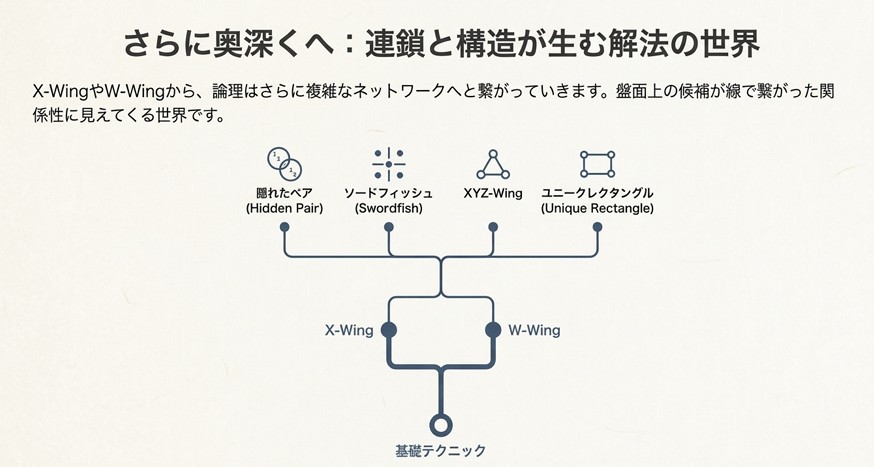
「ここがONならあそこがOFF、だからここはON……」という風に、離れたマス同士の関係から候補を削除したり、確定に繋げたりできるようになります。ここまで来ると、ナンプレは単なる数字埋めではなく、論理パズルとして一段と深みを増してきます。

一意性やユニークレクタングルの活用

これは少しメタ的な（パズルの構造そのものを利用した）解法ですが、非常に強力なのがユニークレクタングル（Unique Rectangle）です。

「答えは一つ」という大前提を利用する

一般的なナンプレ（とくに良問として作られたもの）は、解が1つに定まるように設計されていることが多いです。ユニークレクタングルは、その「唯一解であるはず」という前提を利用して候補を削るテクニックです。

もし盤面に「候補が2つずつの4つのマスが長方形を作る（例：4隅すべてが[1, 9]の候補）」パターンがそのまま残ってしまうと、1と9を入れ替えてもルール上の矛盾が生じず、解が複数成立し得る形になってしまいます（一般にDeadly Patternと呼ばれます）。

「唯一解のパズルなら、その形のまま確定して残ることはないはずだ」という理屈で、候補を削除したり、場合によっては数字を確定させたりします。純粋な“ルールだけ”の推論より一段踏み込むため、使う場面は選びつつ、最終盤の強い武器として覚えておくと行き詰まりを打破しやすくなります。

難問攻略に役立つおすすめアプリとツール

行き詰まった時、ただ答えを見るのではなく「どのテクニックを使えば進むのか」を示してくれるツールを使うのも、効率的な勉強になります。

最近のアプリの中には、ヒント機能で「この局面では○○系のロジックが使える」といった方向性を出してくれるものもあります（表示される内容や粒度はアプリによって差があります）。

また、紙のメモが煩雑になって思考が止まってしまう場合は、一度アプリやPC上に盤面を写して、候補数字をきれいに整理し直すだけでも視界が開け、突破口が見えることがあります。

ナンプレ上級の行き詰まりを解消する思考

最後に、私が上級問題に対峙する時に大切にしているマインドセットをお伝えします。それは、「行き詰まりこそが上達の最大のチャンス」だと捉えることです。

スラスラ解けている時は、すでに自分が知っている手筋の範囲で処理できているだけです。しかし、手が止まった時こそが、新しいロジック（X-WingやW-Wingなど）を習得して、自分の引き出しを増やす瞬間になります。短期間で「型」を作って定着させたいなら、ページを区切って反復する学習法も相性が良いです（参考：反復で知識を定着させる勉強法（第2種衛生管理者の短期対策例））。

「解けない＝悪いこと」と思わず、「お、ついに新しい技を使う出番が来たな」と向き合ってみてください。苦労して糸口を見つけ、盤面が動き出した瞬間の「アハ体験」は、何物にも代えがたい快感ですよ。